How to make a rectangular object perfectly square using PTGui:
The frame is straight, but somehow the photo looks distorted.
The camera (film/sensor) was not exactly parallel to the object during the exposure
and resulted in a slightly skewed frame along with some distortions (bowed lines)
caused by the lens:

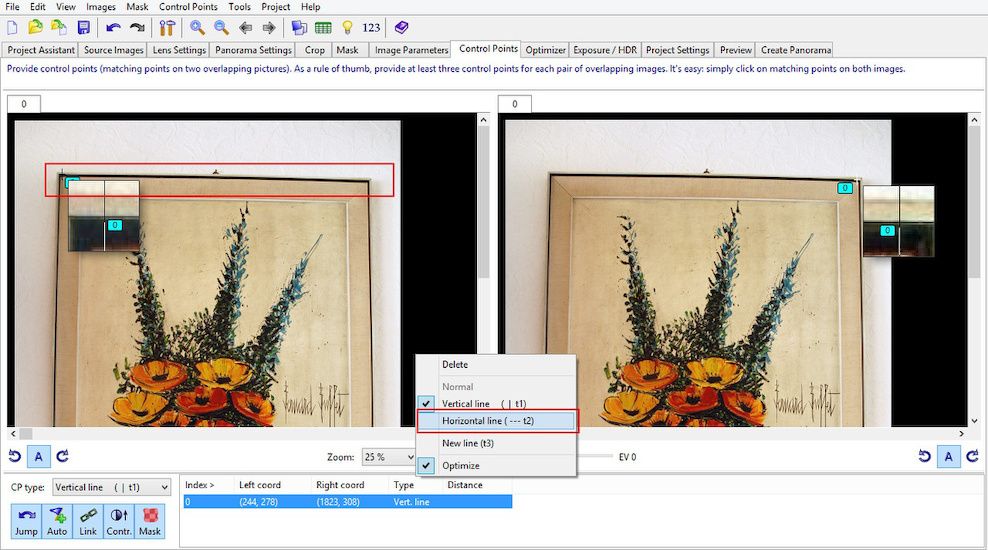
This can easily be fixed with the panotools: start with vertical and horizontal control points.
For this I'm using the PTGui software. Note: by default t1 points (vertical line) are selected.
Change horizontal control points to the t2 type.
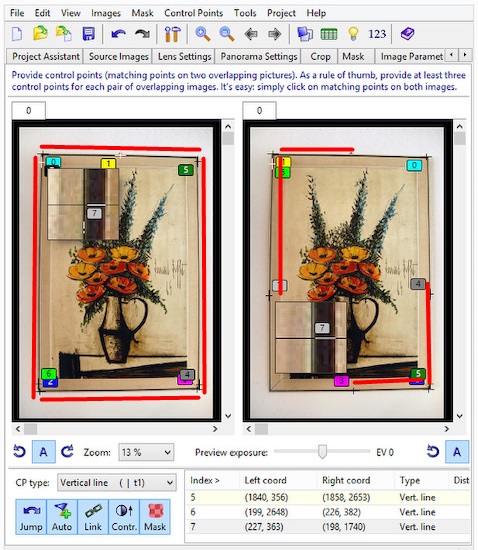
It is important to align vertical and horizontal control points not only at the
corner points but also in the middle of the sides.
Any camera lens has a distortion and lines are not straight. Using the middle
points will fix those bows too.
Make sure the lens type is rectilinear:
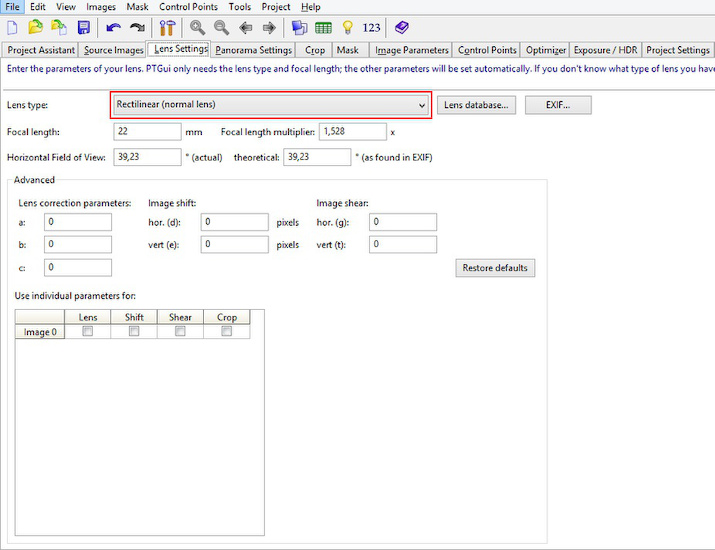
And the projection is set to rectilinear:
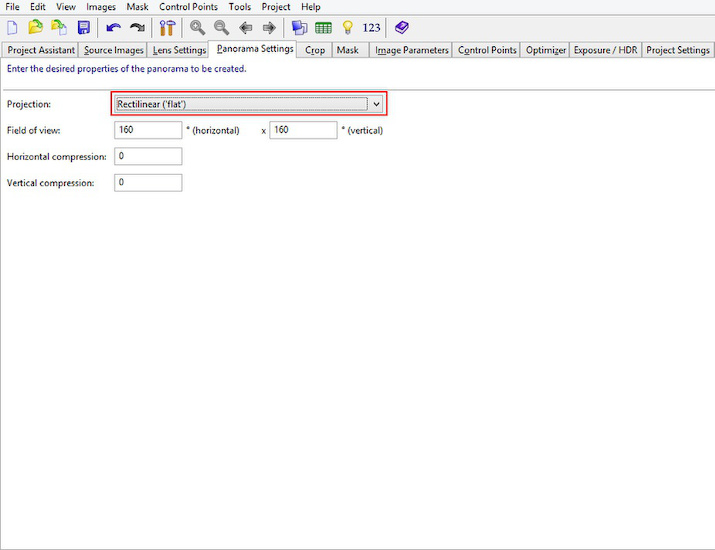
Select Raw, Pitch and Roll and run the first optimization.
It is important not to select all variables at once: optimization is finding
a low spot in a multidimensional field and optimizing for Raw, Pitch and Roll
first you make sure not to optimize on a local spot in a wrong location.
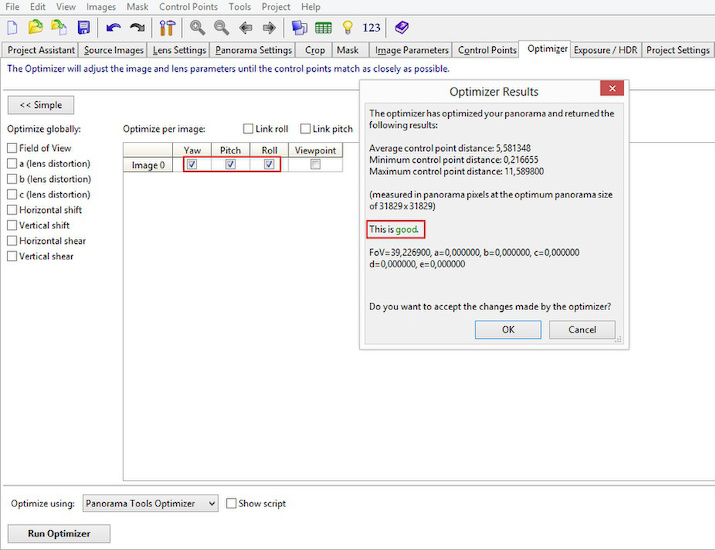
The first result looks good and corners are aligned correctly. Now we fix the bowed lines.
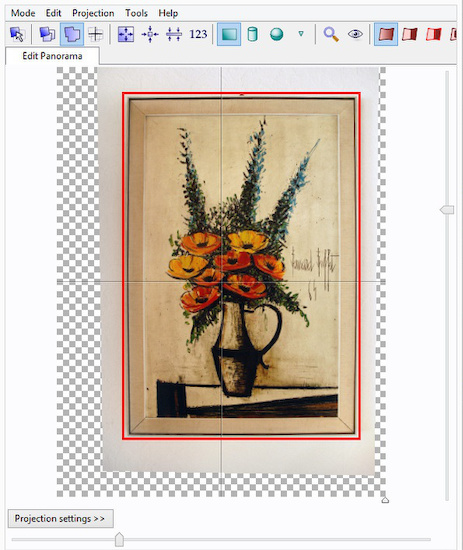
Add the Field of View, b and vert/horz shift.
Do not use a, b and c altogether. Just the b parameter is
perfectly suited for the non-wavy camera lens distortions.
The optimizer can now calculate the exact parameter values:
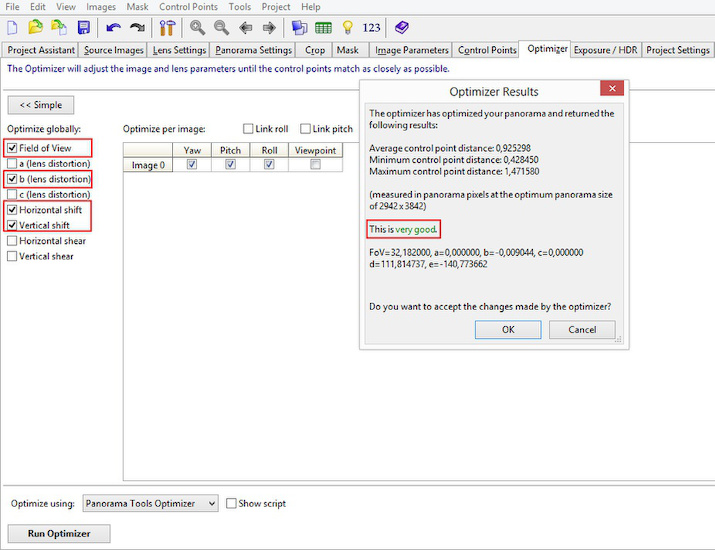
The object is now straitened:
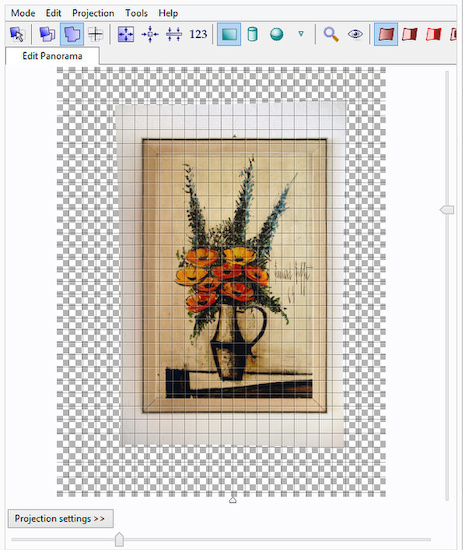
The panotools take all the calculated parameters and create the final output image:
Perfectly square:

A practical exercise with PowerShell.
6 gears with 2 gears of a set of 10 available gears make up the ratio for cutting metric and imperial threads using a G0602 metal lathe.
The gear labels suggest only 24 metric and 29 imperial combinations, but
526 unique combinations from 0,25mm/101,6tpi up to 3,47tpi/7,3169mm are possible.
Gears
The spindle gear at the top all the way down to the leadscrew gear at the bottom:

The leadscrew gear
The leadscrew gear allows 9 different ratios:

Imperial gear label
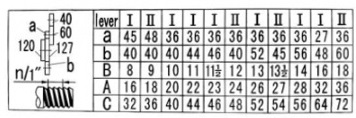
Metric gear label
The script
This PowerShell script creates all gear combinations and outputs the result in a CSV
and TXT file. The CSV contains also all duplicate combinations possible with the different gear ratios.
First all gears combinations are created from a one-dimensional array into a two-dimensional array. The ratios of all gear combinations are connected to the 9 leadscrew ratios. The a and b gear are swapped in the inner loop.
The result is stored in one of PowerShells best inventions: the PSCustomObject. The result of the calculation is a list of PSCustomObjects which can be send directly to a CSV or formatted to a TXT file.
The lead screw has 12 threads per Inch. The conversion from Inch to metric is done by connecting the 'b' gear to the 120 gear instead of the 127 gear.
2 * 127 = 254 -> 1 Inch = 25.4 mm
With the leadscrew gears (III,ABC), the main ratio is a/b * III*ABC. For metric it is 4/3 * ratio and 18 / ratio for imperial.
For each of the values, the matching metric/imperial value is added in brackets. The conversion is rather simple: Metric = 25.4mm*tpi / Imperial and Imperial = 25.4tpi*mm / Metric
# available gears
$z = @(27, 32, 36, 40, 44, 45, 48, 52, 56, 60)
$ab = $null
# create all gear combinations
for ([int]$u = 0; $u -lt $z.length; $u++)
{
for ([int]$v = $u+1; $v -lt $z.length; $v++)
{
$ab += ,($z[$u], $z[$v])
}
}
# leadscrew gear ratio
$ABC = @((1,'A'),(2,'B'),(0.5,'C'))
$III = @((1,'I'),((5/6),'II'),((7/6),'III'))
$t =
foreach ($_ab in $ab)
{
foreach ($_A in $ABC)
{
foreach ($_I in $III)
{
# and swap gear
for ([int]$ab_index = 0; $ab_index -lt 2; $ab_index++)
{
$a = $_ab[$ab_index]
$b = $_ab[1-$ab_index]
$r = $_I[0] * $_A[0] * $a / $b
$mm = $r * 4 / 3
$tpi = 18 / $r
[PSCustomObject]@{
'a' = $a
'b' = $b
'III' = $_I[1]
'ABC' = $_A[1]
'mm' = $mm
'tpi' = $tpi
}
}
}
}
}
# export to CSV
$t | Export-Csv -NoTypeInformation -Delimiter ";" -Encoding UTF8 -Path g0602.csv
# sort for threadsize and write to a text file
$list = $t | sort -Property mm -Unique | % { (" {0}-{1} {2,-3} {3} = {4:0.####}mm ({5:0.##}tpi) {6:0.##}tpi ({7:0.####}mm) " -f $_.a, $_.b, $_.III, $_.ABC, $_.mm, (25.4 / $_.mm), $_.tpi, (25.4 / $_.tpi)) }
$list | Out-File g0602.txt
$list
"{0} Einträge" -f $list.Count
Most combinations are fractional. Here is a filtered metric list (24 entries):
$list_mm = $t | sort -Property mm -Unique | ? { (20*$_.mm - [int](20*$_.mm)) -eq 0
} | % { (" {0}-{1} {2,-3} {3} = {4:0.####}mm ({5:0.##}tpi) " -f $_.a, $_.b, $_.III, $_.ABC, $_.mm, (25.4 / $_.mm), $_.tpi, (25.4 / $_.tpi))
}
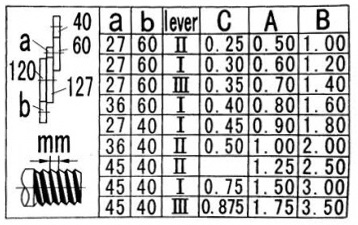
27-60 II C = 0,25mm (101,6tpi)
27-60 I C = 0,3mm (84,67tpi)
27-40 I C = 0,45mm (56,44tpi)
36-40 II C = 0,5mm (50,8tpi)
27-60 I A = 0,6mm (42,33tpi)
45-40 I C = 0,75mm (33,87tpi)
27-40 I A = 0,9mm (28,22tpi)
27-36 I A = 1mm (25,4tpi)
27-40 III A = 1,05mm (24,19tpi)
27-60 I B = 1,2mm (21,17tpi)
36-32 II A = 1,25mm (20,32tpi)
27-48 I B = 1,5mm (16,93tpi)
36-32 III A = 1,75mm (14,51tpi)
27-40 I B = 1,8mm (14,11tpi)
36-48 I B = 2mm (12,7tpi)
27-40 III B = 2,1mm (12,1tpi)
27-32 I B = 2,25mm (11,29tpi)
36-40 I B = 2,4mm (10,58tpi)
45-56 III B = 2,5mm (10,16tpi)
36-32 I B = 3mm (8,47tpi)
36-32 III B = 3,5mm (7,26tpi)
45-32 I B = 3,75mm (6,77tpi)
48-32 I B = 4mm (6,35tpi)
60-32 I B = 5mm (5,08tpi)
Filtered imperial list (56 entries):
$list_tpi = $t | sort -Property mm -Unique | ? { (2*$_.tpi - [int](2*$_.tpi)) -eq 0
} | % { (" {0}-{1} {2,-3} {3} = {6:0.##}tpi ({7:0.####}mm) " -f $_.a, $_.b, $_.III, $_.ABC, $_.mm, (25.4 / $_.mm), $_.tpi, (25.4 / $_.tpi))
}
27-60 II C = 96tpi (0,2646mm)
32-60 II C = 81tpi (0,3136mm)
27-60 I C = 80tpi (0,3175mm)
36-60 II C = 72tpi (0,3528mm)
32-60 I C = 67,5tpi (0,3763mm)
27-40 II C = 64tpi (0,3969mm)
27-56 III C = 64tpi (0,3969mm)
32-56 I C = 63tpi (0,4032mm)
36-60 I C = 60tpi (0,4233mm)
32-52 I C = 58,5tpi (0,4342mm)
36-56 I C = 56tpi (0,4536mm)
36-45 II C = 54tpi (0,4704mm)
32-56 III C = 54tpi (0,4704mm)
36-52 I C = 52tpi (0,4885mm)
32-44 I C = 49,5tpi (0,5131mm)
36-40 II C = 48tpi (0,5292mm)
32-40 I C = 45tpi (0,5644mm)
36-44 I C = 44tpi (0,5773mm)
48-56 I C = 42tpi (0,6048mm)
48-45 II C = 40,5tpi (0,6272mm)
32-60 II A = 40,5tpi (0,6272mm)
27-60 I A = 40tpi (0,635mm)
48-52 I C = 39tpi (0,6513mm)
48-56 III C = 36tpi (0,7056mm)
48-44 I C = 33tpi (0,7697mm)
45-40 I C = 32tpi (0,7938mm)
27-56 III A = 32tpi (0,7938mm)
32-56 I A = 31,5tpi (0,8063mm)
48-40 I C = 30tpi (0,8467mm)
36-56 I A = 28tpi (0,9071mm)
60-45 I C = 27tpi (0,9407mm)
32-56 III A = 27tpi (0,9407mm)
36-52 I A = 26tpi (0,9769mm)
27-36 I A = 24tpi (1,0583mm)
32-40 I A = 22,5tpi (1,1289mm)
36-44 I A = 22tpi (1,1545mm)
48-56 I A = 21tpi (1,2095mm)
27-60 I B = 20tpi (1,27mm)
48-52 I A = 19,5tpi (1,3026mm)
27-45 II B = 18tpi (1,4111mm)
48-44 I A = 16,5tpi (1,5394mm)
27-48 I B = 16tpi (1,5875mm)
27-56 III B = 16tpi (1,5875mm)
36-60 I B = 15tpi (1,6933mm)
36-56 I B = 14tpi (1,8143mm)
48-36 I A = 13,5tpi (1,8815mm)
32-56 III B = 13,5tpi (1,8815mm)
36-52 I B = 13tpi (1,9538mm)
36-48 I B = 12tpi (2,1167mm)
36-44 I B = 11tpi (2,3091mm)
48-56 I B = 10,5tpi (2,419mm)
36-40 I B = 10tpi (2,54mm)
48-56 III B = 9tpi (2,8222mm)
36-32 I B = 8tpi (3,175mm)
48-40 I B = 7,5tpi (3,3867mm)
48-32 I B = 6tpi (4,2333mm)
All 526 entries as a text file sorted by size.
The metric column is the size with the 'b' gear connected to the 120.
The imperial column is the size with the 'b' gear connected to the 127.
'a'-'b' leadscrew gear = metric column imperial column
27-60 II C = 0,25mm (101,6tpi) 96tpi (0,2646mm)
27-56 II C = 0,2679mm (94,83tpi) 89,6tpi (0,2835mm)
27-52 II C = 0,2885mm (88,05tpi) 83,2tpi (0,3053mm)
32-60 II C = 0,2963mm (85,73tpi) 81tpi (0,3136mm)
27-60 I C = 0,3mm (84,67tpi) 80tpi (0,3175mm)
27-48 II C = 0,3125mm (81,28tpi) 76,8tpi (0,3307mm)
:
:
60-27 II B = 4,9383mm (5,14tpi) 4,86tpi (5,2263mm)
60-32 I B = 5mm (5,08tpi) 4,8tpi (5,2917mm)
52-32 III B = 5,0556mm (5,02tpi) 4,75tpi (5,3505mm)
44-27 III B = 5,07mm (5,01tpi) 4,73tpi (5,3657mm)
52-27 I B = 5,1358mm (4,95tpi) 4,67tpi (5,4354mm)
45-27 III B = 5,1852mm (4,9tpi) 4,63tpi (5,4877mm)
56-32 III B = 5,4444mm (4,67tpi) 4,41tpi (5,762mm)
56-27 I B = 5,5309mm (4,59tpi) 4,34tpi (5,8535mm)
60-32 III B = 5,8333mm (4,35tpi) 4,11tpi (6,1736mm)
60-27 I B = 5,9259mm (4,29tpi) 4,05tpi (6,2716mm)
52-27 III B = 5,9918mm (4,24tpi) 4,01tpi (6,3413mm)
56-27 III B = 6,4527mm (3,94tpi) 3,72tpi (6,8291mm)
60-27 III B = 6,9136mm (3,67tpi) 3,47tpi (7,3169mm)